Midterm Review
CSE-4/562 Spring 2019
March 11, 2019
What are Databases?
- Analysis: Answering user-provided questions about data
- What kind of tools can we give end-users?
- Declarative Languages
- Organizational Datastructures (e.g., Indexes)
- Manipulation: Safely persisting and sharing data updates
- What kind of tools can we give end-users?
- Consistency Primitives
- Data Validation Primitives
- Primitive
- Basic building blocks like Int, Float, Char, String
- Tuple
- Several ‘fields’ of different types. (N-Tuple = N fields)
- A Tuple has a ‘schema’ defining each field
- Set
- A collection of unique records, all of the same type
- Bag
- An unordered collection of records, all of the same type
- List
- An ordered collection of records, all of the same type
SELECT [DISTINCT] targetlist
FROM relationlist
WHERE condition
- Compute the $2^n$ combinations of tuples in all relations appearing in relationlist
- Discard tuples that fail the condition
- Delete attributes not in targetlist
- If DISTINCT is specified, eliminate duplicate rows
This is the least efficient strategy to compute a query! A good optimizer will find more efficient strategies to compute the same answer.
Physical Layout
Record Formats
- Fixed
- Constant-size fields. Field $i$ at byte $\sum_{j < i} |Field_j|$
- Delimited
- Special character or string (e.g.,
,) between fields - Header
- Fixed-size header points to start of each field
File Formats
- Fixed
- Constant-size records. Record $i$ at byte $|Record| \times i$
- Delimited
- Special character or string (e.g.,
\r\n) at record end - Header
- Index in file points to start of each record
- Paged
- Align records to paging boundaries
- File
- A collection of pages (or records)
- Page
- A fixed-size collection of records
- Page size is usually dictated by hardware.
Mem Page $\approx$ 4KB Cache Line $\approx$ 64B - Record
- One or more fields (for now)
- Field
- A primitive value (for now)
Relational Algebra
Relational Algebra
| Operation | Sym | Meaning |
|---|---|---|
| Selection | $\sigma$ | Select a subset of the input rows |
| Projection | $\pi$ | Delete unwanted columns |
| Cross-product | $\times$ | Combine two relations |
| Set-difference | $-$ | Tuples in Rel 1, but not Rel 2 |
| Union | $\cup$ | Tuples either in Rel 1 or in Rel 2 |
| Intersection | $\cap$ | Tuples in both Rel 1 and Rel 2 |
| Join | $\bowtie$ | Pairs of tuples matching a specified condition |
| Division | $/$ | "Inverse" of cross-product |
| Sort | $\tau_A$ | Sort records by attribute(s) $A$ |
| Limit | $\texttt{LIMIT}_N$ | Return only the first $N$ records (according to sort order if paired with sort). |
Equivalence
$$Q_1 = \pi_{A}\left( \sigma_{c}( R ) \right)$$ $$Q_2 = \sigma_{c}\left( \pi_{A}( R ) \right)$$| Rule | Notes |
|---|---|
| $\sigma_{C_1\wedge C_2}(R) \equiv \sigma_{C_1}(\sigma_{C_2}(R))$ | |
| $\sigma_{C_1\vee C_2}(R) \equiv \sigma_{C_1}(R) \cup \sigma_{C_2}(R)$ | Only true for set, not bag union |
| $\sigma_C(R \times S) \equiv R \bowtie_C S$ | |
| $\sigma_C(R \times S) \equiv \sigma_C(R) \times S$ | If $C$ references only $R$'s attributes, also works for joins |
| $\pi_{A}(\pi_{A \cup B}(R)) \equiv \pi_{A}(R)$ | |
| $\sigma_C(\pi_{A}(R)) \equiv \pi_A(\sigma_C(R))$ | If $A$ contains all of the attributes referenced by $C$ |
| $\pi_{A\cup B}(R\times S) \equiv \pi_A(R) \times \pi_B(S)$ | Where $A$ (resp., $B$) contains attributes in $R$ (resp., $S$) |
| $R \times (S \times T) \equiv (R \times S) \times T$ | Also works for joins |
| $R \times S \equiv S \times R$ | Also works for joins |
| $R \cup (S \cup T) \equiv (R \cup S) \cup T$ | Also works for intersection and bag-union |
| $R \cup S \equiv S \cup R$ | Also works for intersections and bag-union |
| $\sigma_{C}(R \cup S) \equiv \sigma_{C}(R) \cup \sigma_{C}(S)$ | Also works for intersections and bag-union |
| $\pi_{A}(R \cup S) \equiv \pi_{A}(R) \cup \pi_{A}(S)$ | Also works for intersections and bag-union |
| $\sigma_{C}(\gamma_{A, AGG}(R)) \equiv \gamma_{A, AGG}(\sigma_{C}(R))$ | If $A$ contains all of the attributes referenced by $C$ |
Algorithms
- "Volcano" Operators (Iterators)
- Operators "pull" tuples, one-at-a-time, from their children.
- 2-Pass (External) Sort
- Create sorted runs, then repeatedly merge runs
- Join Algorithms
- Quickly picking out specific pairs of tuples.
- Aggregation Algorithms
- In-Memory vs 2-Pass, Normal vs Group-By
Nested-Loop Join
Block-Nested Loop Join
Strategies for Implementing $R \bowtie_{R.A = S.A} S$
- Sort/Merge Join
- Sort all of the data upfront, then scan over both sides.
- In-Memory Index Join (1-pass Hash; Hash Join)
- Build an in-memory index on one table, scan the other.
- Partition Join (2-pass Hash; External Hash Join)
- Partition both sides so that tuples don't join across partitions.
Sort/Merge Join
Sort/Merge Join
Sort/Merge Join
Sort/Merge typically expressed as 3 operators
(2xSort + Merge)
1-Pass Hash Join
2-Pass Hash Join
- Limited Queries
- Only supports join conditions of the form $R.A = S.B$
- Low Memory
- Never need more than 1 pair of partitions in memory
- High IO Cost
- Every record gets written out to disk, and back in.
Can partition on data-values to support other types of queries.
Index Nested Loop Join
To compute $R \bowtie_{R.A < S.B} S$ with an index on $S.B$- Read One Row of $R$
- Get the value of $R.A$
- Start index scan on $S.B > [R.A]$
- Return rows as normal
Basic Aggregate Pattern
- Init
- Define a starting value for the accumulator
- Fold(Accum, New)
- Merge a new value into the accumulator
- Finalize(Accum)
- Extract the aggregate from the accumulator.
Basic Aggregate Types
Grey et. al. "Data Cube: A Relational Aggregation Operator Generalizing Group-By, Cross-Tab, and Sub-Totals
- Distributive
- Finite-sized accumulator and doesn't need a finalize (COUNT, SUM)
- Algebraic
- Finite-sized accumulator but needs a finalize (AVG)
- Holistic
- Unbounded accumulator (MEDIAN)
Grouping Algorithms
- 2-pass Hash Aggregate
- Like 2-pass Hash Join: Distribute groups across buckets, then do an in-memory aggregate for each bucket.
- Sort-Aggregate
- Like Sort-Merge Join: Sort data by groups, then group elements will be adjacent.
Indexing
Data Organization
- Unordered Heap
- No organization at all. $O(N)$ reads.
- (Secondary) Index
- Index structure over unorganized data. $O(\ll N)$ random reads for some queries.
- Clustered (Primary) Index
- Index structure over clustered data. $O(\ll N)$ sequential reads for some queries.
Data Organization
Data Organization
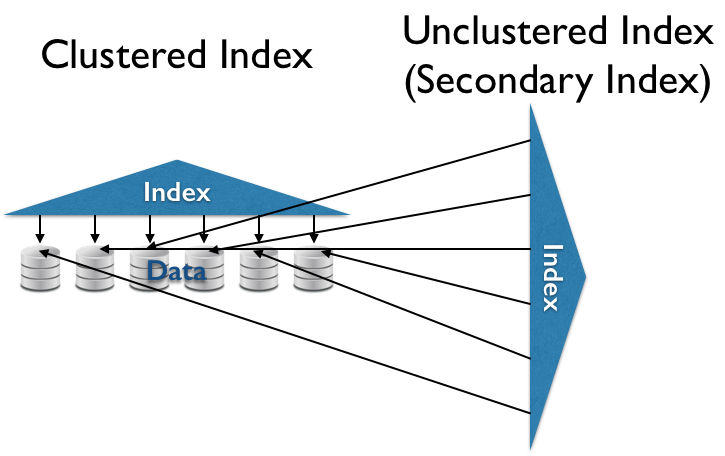
Tree-Based Indexes
Rules of B+Trees
- Keep space open for insertions in inner/data nodes.
- ‘Split’ nodes when they’re full
- Avoid under-using space
- ‘Merge’ nodes when they’re under-filled
Maintain Invariant: All Nodes ≥ 50% Full
(Exception: The Root)
Problems
- $N$ is too small
- Too many overflow pages (slower reads).
- $N$ is too big
- Too many normal pages (wasted space).
Problems
- Changing hash functions reallocates everything
- Only double/halve the size of a hash function
- Changing sizes still requires reading everything
- Idea: Only redistribute buckets that are too big
Cost-Based Optimization
Accounting
Figure out the cost of each individual operator.
Only count the number of IOs added by each operator.
| Operation | RA | IOs Added (#pages) | Memory (#tuples) |
|---|---|---|---|
| Table Scan | $R$ | $\frac{|R|}{\mathcal P}$ | $O(1)$ |
| Projection | $\pi(R)$ | $0$ | $O(1)$ |
| Selection | $\sigma(R)$ | $0$ | $O(1)$ |
| Union | $R \uplus S$ | $0$ | $O(1)$ |
| Sort (In-Mem) | $\tau(R)$ | $0$ | $O(|R|)$ |
| Sort (On-Disk) | $\tau(R)$ | $\frac{2 \cdot \lfloor log_{\mathcal B}(|R|) \rfloor}{\mathcal P}$ | $O(\mathcal B)$ |
| (B+Tree) Index Scan | $Index(R, c)$ | $\log_{\mathcal I}(|R|) + \frac{|\sigma_c(R)|}{\mathcal P}$ | $O(1)$ |
| (Hash) Index Scan | $Index(R, c)$ | $1$ | $O(1)$ |
- Tuples per Page ($\mathcal P$) – Normally defined per-schema
- Size of $R$ ($|R|$)
- Pages of Buffer ($\mathcal B$)
- Keys per Index Page ($\mathcal I$)
| Operation | RA | IOs Added (#pages) | Memory (#tuples) |
|---|---|---|---|
| Nested Loop Join (Buffer $S$ in mem) | $R \times S$ | $0$ | $O(|S|)$ |
| Nested Loop Join (Buffer $S$ on disk) | $R \times_{disk} S$ | $(1+ |R|) \cdot \frac{|S|}{\mathcal P}$ | $O(1)$ |
| 1-Pass Hash Join | $R \bowtie_{1PH, c} S$ | $0$ | $O(|S|)$ |
| 2-Pass Hash Join | $R \bowtie_{2PH, c} S$ | $\frac{2|R| + 2|S|}{\mathcal P}$ | $O(1)$ |
| Sort-Merge Join | $R \bowtie_{SM, c} S$ | [Sort] | [Sort] |
| (Tree) Index NLJ | $R \bowtie_{INL, c}$ | $|R| \cdot (\log_{\mathcal I}(|S|) + \frac{|\sigma_c(S)|}{\mathcal P})$ | $O(1)$ |
| (Hash) Index NLJ | $R \bowtie_{INL, c}$ | $|R| \cdot 1$ | $O(1)$ |
| (In-Mem) Aggregate | $\gamma_A(R)$ | $0$ | $adom(A)$ |
| (Sort/Merge) Aggregate | $\gamma_A(R)$ | [Sort] | [Sort] |
- Tuples per Page ($\mathcal P$) – Normally defined per-schema
- Size of $R$ ($|R|$)
- Pages of Buffer ($\mathcal B$)
- Keys per Index Page ($\mathcal I$)
- Number of distinct values of $A$ ($adom(A)$)
Estimating IOs requires Estimating $|Q(R)|$
| Operator | RA | Estimated Size |
|---|---|---|
| Table | $R$ | $|R|$ |
| Projection | $\pi(Q)$ | $|Q|$ |
| Union | $Q_1 \uplus Q_2$ | $|Q_1| + |Q_2|$ |
| Cross Product | $Q_1 \times Q_2$ | $|Q_1| \times |Q_2|$ |
| Sort | $\tau(Q)$ | $|Q|$ |
| Limit | $\texttt{LIMIT}_N(Q)$ | $N$ |
| Selection | $\sigma_c(Q)$ | $|Q| \times \texttt{SEL}(c, Q)$ |
| Join | $Q_1 \bowtie_c Q_2$ | $|Q_1| \times |Q_2| \times \texttt{SEL}(c, Q_1\times Q_2)$ |
| Distinct | $\delta_A(Q)$ | $\texttt{UNIQ}(A, Q)$ |
| Aggregate | $\gamma_{A, B \leftarrow \Sigma}(Q)$ | $\texttt{UNIQ}(A, Q)$ |
- $\texttt{SEL}(c, Q)$: Selectivity of $c$ on $Q$, or $\frac{|\sigma_c(Q)|}{|Q|}$
- $\texttt{UNIQ}(A, Q)$: # of distinct values of $A$ in $Q$.
(Some) Estimation Techniques
- Guess Randomly
- Rules of thumb if you have no other options...
- Uniform Prior
- Use basic statistics to make a very rough guess.
- Sampling / History
- Small, Quick Sampling Runs (or prior executions of the query).
- Histograms
- Using more detailed statistics for improved guesses.
- Constraints
- Using rules about the data for improved guesses.
Sketching
| Flips | Score | Probability | E[# Games] |
|---|---|---|---|
| (👽) | 0 | 0.5 | 2 |
| (🐕)(👽) | 1 | 0.25 | 4 |
| (🐕)(🐕)(👽) | 2 | 0.125 | 8 |
| (🐕)$\times N$ (👽) | $N$ | $\frac{1}{2^{N+1}}$ | $2^{N+1}$ |
If I told you that in a series of games, my best score was $N$, you might expect that I played $2^{N+1}$ games.
To do that, I only need to track my top score!
Flajolet-Martin Sketches
($\approx$ HyperLogLog)
- For each record...
- Hash each record
- Find the index of the lowest-order non-zero bit
- Add the index of the bit to a set
- Find $R$, the lowest index not in the set
- Estimate Count-Distinct as $\frac{2^R}{\phi}$ ($\phi \approx 0.77351$)
- Repeat (in parallel) as needed
Count Sketches
- Pick a number of "trials" and a number of "bins"
- For each record $O_i$
- For each "trial" $j$
- Use a hash function $h_j(O_i)$ to pick a bin
- Add a $\pm 1$ value determined by hash function $\delta_j(O_i)$ to the bin
- For each "trial" $j$
Count-Min Sketches
- Pick a number of "trials" and a number of "bins"
- For each record $O_i$
- For each "trial" $j$
- Use a hash function $h_j(O_i)$ to pick a bin
- Add 1 to the bin
- For each "trial" $j$
- Flajolet-Martin Sketches (HyperLogLog)
- Estimating Count-Distinct
- Count Sketches
- Estimating Count-GroupBy
(roughly uniform counts) - Count-Min Sketches
- Estimating Count-GroupBy
(small number of heavy hitters)
The WINDOW Operator
- Define a Sequence (i.e., sort the relation)
- Compute all subsequences
- Fixed Physical Size: N records exactly.
- Fixed Logical Size: Records within N units of time.
- Compute an aggregate for each subsequence (one output row per subsequence)
SELECT L.state, T.month,
AVG(S.sales) OVER W as movavg
FROM Sales S, Times T, Locations L
WHERE S.timeid = T.timeid
AND S.locid = L.locid
WINDOW W AS (
PARTITION BY L.state
ORDER BY T.month
RANGE BETWEEN INTERVAL ‘1’ MONTH PRECEDING
AND INTERVAL ‘1’ MONTH FOLLOWING
)
Summary
- Push vs Pull Data Flow
- Push is a better fit because sources produce data at different rates.
- Revisit Joins
- Focus on ripple-style
WINDOWjoins. - Revisit Indexing
- Linked Hash/Tree Indexes for efficient windowed indexing.
- Revisit Aggregation
- Sliding window aggregates.